Understanding is about making connection. The extent to which a concept is understood is a function of the strength of its connection with other concepts. An isolated piece of knowledge is not powerful.
To understand mathematics is to make connections among concepts, procedures, contexts. A lesson that has a very good potential for learning a well-connected mathematical knowledge is one which is organized around a mathematical investigation. This is because of the divergence nature of this task which revolves around a single tool or context.
Here is a simple investigation activity about polygons. Change the x by x unit to 1 by 1 unit if you will give this to Grade 5-6 students.
Investigate polygons with area 5x^2 units on an x by x unit grid.
Some initial shapes students could come up with may look like the following:

Note: This is a mathematical investigation so the students are expected to pose the problems they want to pursue and on how they will solve it. It will cease to be a math investigation if the teachers will be the one to pose the problems for them. The following are sample problems that students can pose for themselves.
- What is the same and what is different among these polygons? How can I classify these polygons?
Possible classifications would be
a. convex vs non-convex polygons
b. according to the number of sides
- What shapes and how many are there if I only consider polygons made up of squares?
Students will discover that while they can have as many polygons with an area of 5, there are only 12 polygons made of squares. This is shown in Figure 2. These shapes are called pentominoes because it is made up of 5 squares. I have arranged it here for easy recall of shapes. It contains the last seven letters of the english alphabet (TUVWKXZ) and the word FILIPINO without the last 2 I’s and O in the spelling.

- Is there a way of constructing different triangles or any of the polygons with same area?
Figure 3 shows this process for triangle.
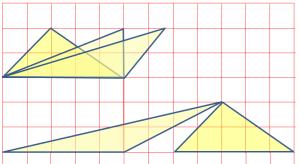
Click this or the figure below to see this process in dynamic mode using Geogebra.

Possible extension of this investigation is to consider polygons with areas other than .
Click this link to see some ideas on how you can use this activity to teach combining algebraic expressions.

I am thankful that you are passionate to share what you have. Thank you you ma’m. I will see to it that your labor is not in vain i am ready to share it with my students. God bless you always!
I wish to thank you for all your work on this blog. I work in a middle school in Italy and I am learning a lot surfing and studying your blog.
Thanks a lot.
Gianfranco
I’m happy to know that. Thank you for appreciating this blog.
Thank you so much. You’re a great help…
Thanks a lot. Finally, this is a site I’ve been looking for to assist my son’s math lessons. What you write is really great help. God bless.
thnx so much!!!! it helps me a lot!!!! tnx!!!
^_^ !!!!! your a good one!!! keep it up!
god bless! and once again thank you!!!!!
many thanks, too:-)
Thanks a lot! That was a really informative blog and you helped me get some more insight on how I can create my own investigatory project since my group and I are having a hard time…. Keep up the great work.
This is a great post. This gives me some great ideas on teaching the area polygons in the future.
Kudos,
Mr. Pi
thanks
Just want to say what a great blog you got here!
I’ve been around for quite a lot of time, but finally decided to show my appreciation of your work!
Thumbs up, and keep it going!
Cheers
Christian
Hi just stumbled your blog and i thank you for your story it was informative. I am interested about doing link building for my site too. Have you used the scrapebox.com tool? If so is it good? If not then what is the best program? Thank you.
Outstanding blogging. Your links with this are wonderful. I went throughout all this as well as I definitely many thanks for the advise.