Understanding is about making connection. The extent to which a concept is understood is a function of the strength of its connection with other concepts. An isolated piece of knowledge is not powerful.
To understand mathematics is to make connections among concepts, procedures, contexts. A lesson that has a very good potential for learning a well-connected mathematical knowledge is one which is organized around a mathematical investigation. This is because of the divergence nature of this task which revolves around a single tool or context.
Here is a simple investigation activity about polygons. Change the x by x unit to 1 by 1 unit if you will give this to Grade 5-6 students.
Investigate polygons with area 5x^2 units on an x by x unit grid.
Some initial shapes students could come up with may look like the following:

Note: This is a mathematical investigation so the students are expected to pose the problems they want to pursue and on how they will solve it. It will cease to be a math investigation if the teachers will be the one to pose the problems for them. The following are sample problems that students can pose for themselves.
- What is the same and what is different among these polygons? How can I classify these polygons?
Possible classifications would be
a. convex vs non-convex polygons
b. according to the number of sides
- What shapes and how many are there if I only consider polygons made up of squares?
Students will discover that while they can have as many polygons with an area of 5, there are only 12 polygons made of squares. This is shown in Figure 2. These shapes are called pentominoes because it is made up of 5 squares. I have arranged it here for easy recall of shapes. It contains the last seven letters of the english alphabet (TUVWKXZ) and the word FILIPINO without the last 2 I’s and O in the spelling.

- Is there a way of constructing different triangles or any of the polygons with same area?
Figure 3 shows this process for triangle.
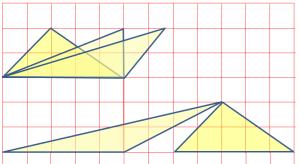
Click this or the figure below to see this process in dynamic mode using Geogebra.

Possible extension of this investigation is to consider polygons with areas other than .
Click this link to see some ideas on how you can use this activity to teach combining algebraic expressions.
