geogebra applet Archives - Mathematics for Teaching

Christmas GeoGebra Applet

Posted on by

Here’s wishing you the choicest blessings of the season. The applet was adapted from the work of Wengler published in GeoGebra Tube. Being an incurable math teacher and blogger I can’t help not to turn this unsuspecting christmas geogebra applet into a mathematical task.

Observe the candles.

1. When is the next candle lighted?

2. On the same coordinate axes, sketch the time vs height graph of each of the four candles?

3. What kind of function does each graph represents? Write the equation of each function?

3. If the candles burns at the rate of 2 cm per second and all the candles are completely burned after 20 seconds, what is the height of each candle? (Note: These are fast burning candles 🙂 )

[iframe https://math4teaching.com/wp-content/uploads/2012/12/PEACE.html 650 700]

Algebra

Solving quadratic equations by completing the square

Posted on by

I’m not a fan of teaching the quadratic formula for solving the roots of quadratic equations because the sight of the outrageous formula itself is enough to make students wish they are invisible in their algebra class. Indeed who wants to have to do withOf course not all quadratic equations can be solved by factoring. Here’s how I try to resolve the situation. Before quadratics, students have been solving linear equations. 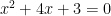So if you ask them to solve $x^2+4x-3 = 0$ , chances are, they will use the same technique they learned earlier and this is to put all the x‘s on one side of the equation and the constants on the other side. They will not think of factoring the expression on the left even if they have done hundreds of factoring exercises earlier. For them factoring is another way of representing an algebraic expression and indeed it is. Solving equation means to find the value of x and based on their earlier experience, the technique is to put the x on one side. So this is what they will do:

$x^2+4x+3=0$

=> $x^2 +4x=-3$

=> $x(x+4)=-3$

Students will try to guess and check until they find the values of x that will make the equation true. They will continue to use this technique until you give them something like $x^2+4x-3=0$ which will make the procedure very tedious. 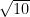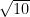This will be the time to prompt them to think of how easy it would be if the one of the side where the x’s are is a perfect square like in $x^2=10$ where $x =$ + $\sqrt{10}$ or in $(x+2)^2 = 10$ so that they will have $x+2=$ + $\sqrt{10}$ . So the problem now is to make the side 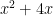$x^2+4x$ a perfect square. A visual representation of the equation will be handy. Students should have no problem thinking of a rectangle as visual representation of a product.

Clearly the left hand side is not a square. The way to make one is to cut-off half of the 4x area. But it makes an incomplete square!

Let’s complete it by adding a 2 by 2 square. To keep the balance we add the same amount on the right hand side.

It should be now easy solving for x by extracting the root and using the properties of equality.

I believe that this process will make sense more than using the quadratic formula. Students just memorize the formula without understanding. They also will not remember a piece of it the next day anyway. I’m not saying the quadratic fomula is not completely useful. One application of it is on using the Cosine Rule for ambiguous case.

Should the method of factoring be taught first? I believe it’s best to introduce the students to the method of completing the square first (with the visuals, of course). Once the students get the hang of this procedure, the first thing that they will drop is drawing the rectangle and square and just do it mentally.You can later ask them to investigate the structure of quadratic equations where it is no longer necessary to transfer the constant on the other side. Solving quadratic equation by factoring therefore is a shortcut students should deduce from the procedure of completing the square.

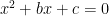Any new procedure should be linked to previously learned procedure or it should be an improvement of the first. This is my reason why I think the process I described above is a natural sequence to the process of solving linear equation that students already learned. Another reason is that most of the problems students encounter involving quadratic equation is of the form $x^2 +bx=c$ rather than $x^2+bx+c=0$ . For example, “Two numbers differ by 4 and their product is 3. What are the two numbers?” The major reason of course is that it will always work for all quadratic equations. 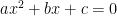Check out the visuals for solving $ax^2+bx+c=0$ .

I also developed a geogebra applets Completing the Square Solver and Quadratic Equation Solver that I posted in AgIMat. You can use them to solve quadratic equations and to investigate their roots.

Algebra, GeoGebra worksheets, Math Lessons

Teaching maximum area problem with GeoGebra

Posted on by

Remember that classic maximum area problem? Here’s a version of it: Pam wishes to fence off a rectangular vegetable garden in her backyard. She has 18 meters of fencing wire which she will use to fence three sides of the garden with the existing fence forming the fourth side. Calculate the maximum area she can enclose.

This problem is usually given as an application problem and is solved algebraically. For example if x is one of the two equal sides to be fenced then the area is the function f(x) = x (18-2x). The maximum area can be found by graphing or by inspection. If students have done a bit of calculus already then they can use the first derivate to solve the problem. But with free technology such as GeoGebra, there should be no excuse not to make the teaching of this topic less abstract especially for Year 9 or 10 students. It need not be at the end of the chapter on quadratic but as an introductory lesson for quadratics. Here’s a GeoGebra applet I made which can be used to teach this topic more visually and conceptually. Below is the image of the applet. I did not embed the applet here because it takes a while to load. Click maximum_area_problem worksheet to explore.

Here’s my suggested teaching approach using this applet. Students need to be given a bit of time exploring it before asking them the following questions:

Pam wishes to fence off a rectangular vegetable garden in her backyard. She found fencing wires stored in their garage which she will use to fence three sides of the garden with the existing fence forming the fourth side. How long is Pam’s fencing wire? What are some of the sizes of gardens Pam can have with the fencing wires?
If you were Pam, what garden size will you choose? Why?
What do the coordinates of P represent? How about the path of P, what information can we get from it?
As the length of BD changes so does the length of the other two sides. What equation will describe the relationship between the length of BD and EF? between BD and DE? between BD and area BDEF.
What equation of function will run through the path of P? Type it in the input bar to check.
What does the tip of the graph tell you about the area of the garden?

Feel free to use the comments sections for other questions and suggestions for teaching this topic. How to teach the derivative function without really trying is a good sequel to this lesson. More lessons in Math Lessons in Mathematics for Teaching.

Share!

Share!

Share!