Posted in Geogebra, Math blogs

Math and Multimedia Carnival # 17 will be hosted here

Posted on by

Hello bloggers. It’s carnival time again. The 17th edition of Math and Multimedia Carnival will be over here at Mathematics for Teaching. It will go live on 28th November 2011.

You are most welcome to share your posts about mathematics and the teaching and learning of it. You can submit your posts in Math and Multimedia Blog Carnival #17 .

Wondering what on earth a math carnival is? Check out these out: (No, not Zac Efron, the carnivals). But if you want to see Zac, check out the dvd 17  Again.

Please Like, Tweet, and Share so more bloggers will know. Thanks.

Posted in What is mathematics

Can having fun and learning math coexist?

Posted on by

I wrote a little post titled Mathematics is not easy  to challenge the teachers I work with to rethink the way they teach mathematics. I  shared the post in LinkedIn and it generated intelligent discussions and ideas about mathematics and teaching mathematics from the community Math, Math Education, Math Culture. I think we can learn a lot from the well-thought of comments and reactions from the community. There are so far 224 comments. Let me share the comments and reactions related to the existence of ‘fun’ in mathematics. Before you read the comments and reactions, I suggest you first read the post Math is not easy.

  1. Certainly not a waste of time. Making it fun and easy has great benefits, such as increased love for math overall, stronger levels of confidence, and an encouragement toward number sense – Steve Kleinrichert
  2. So are you suggesting that we just tell our students on day one that “this is not going to be a fun class. This material is going to be difficult and you probably won’t understand it!”…..
    And what is your “fact” based on? “Math is not an easy subject”… With proper techniques & approaches, math can be as easy as any other subject. And “… not easy to learn it” depends on the student, teacher & learning goals.
    Also, if you are suggesting that teachers accept the “fact”, how will that make it better for anyone, students or teachers? – Scott Taylor.
  3. There’s a big difference between making math fun by putting in external wastes of time that obscure the math, and making it fun *because* of the mathematics and the interesting problems within. I agree that we shouldn’t do the former, which I think is what Erlina is saying. But we should try to choose problems that are fun and engaging through their mathematical content. – Daniel Zaharopol.
  4. So much mathematics can be learnt through a playful interaction with the problem. In fact, we often colour our students perception of what we expect by using words like problem when puzzle or dilemma would be just as suitable. A sense of fun is, in my experience, essential as it prevents students from giving up and writing off the ability that they have already. – Mike Chittenden
  5. Making mathematics easy is the goal of every diligent math teacher. Like perfection, the ideal may be unattainable but the pursuit is worthy. – Charles Ashbacher
  6. I also disagree with you. If teachers stopped trying to make math fun I think math would get even more boring. There is so much beauty and mystery. I asked my students what they thought math was and they gave some very interesting answers. Since I am teaching in China none of my students said stupid or not fun. There is fun to be had and interesting things to talk about. – Dominique Lomax
  7. My mathematics teachers did not try to make mathematics fun, yet I found that mathematics is interesting in itself. – Ng Foo Keong (Sophus)
  8. Math and any other subject can be difficult / boring / not fun depending on our (teachers) goals. I have never pretended that I educate new generation of mathematicians. My goal is to develop the way of mathematical thinking through delivering strong basis of mathematical concepts. Can it be fun? Maybe. Is it difficult? For whom: teachers or students? It depends on…. Lots of parameters. – Bess Ostrovsky

More related insights in The fun in learning mathematics is in the challenge.

Posted in Algebra

Visual representations of the difference of two squares

Posted on by

Students’ understanding of mathematics is a function of the quality and quantity of the connections of a concept with other concepts. As I always say in this blog, ‘To understand is to make connections’.

There are many ways  of helping students make connections. One of these is through activities involving multiple representations. Here is a lesson you can use for teaching the difference of two squares, x^2-y^2.

Activity: Ask the class to cut off a square from the corner of a square piece of paper. If this is given in the elementary grades, you can use papers with grid. If you give it to Grade 7 or 8 students you can use x for the side of the big square and y for the side of the smaller square. Challenge the class to find different ways of calculating the area of the remaining piece. Below are two possible solutions

Solution 1 – Dissect into two rectangles

 

Solution 2 – Dissect into two congruent trapezoids to form a rectangle

 

Extend the problem by giving them a square paper with a square hole in the middle and ask them to represent the area of the remaining piece, in symbols and geometrically.

Solution 1 – Dissect into four congruent trapezoids to form a parallelogram

 

Solution 2 – Dissect into 4 congruent rectangles to form a bigger rectangle

These two problems about the difference of two squares will not only help students connect algebra and geometry concepts. It also develop their visualization skills.

This is a problem solving activity. It’s important to give your students time to think. Simply using this to illustrate the factors of the difference of two squares will be depriving students to engage in thinking. They may find it a little difficult to represent the dimensions of the shapes but I’m sure they can dissect the shapes. Trust me.

Posted in Combinatorics, High school mathematics

Linking combination and permutation with repetition

Posted on by

Combinatorial problems are difficult because it’s hard to  know which formula to use in a particular problem and when you need to ‘tweak’ or totally abandon the formula. In this post I share two solutions to a problem which connects the multiplication  principle, the combination formula and the formula for counting the number of permutation with repetition. Knowledge of connections among concepts help in problem solving. The problem is generated from the rook puzzle presented in my post Connecting Pascal’s Triangle and Permutation with identical objects.

Find the number of different ways of arranging 14 letters 7 of which are E’s and 7 are N’s, in a row. Here is one arrangement:

The first solution shows how the formula for counting permutation with identical objects can be deduced from the solution involving the multiplication principle and the second connects permutation and combination.

Solution 1

The idea behind this solution is to initially treat each letter as distinct. There are 14 letters to be arranged in a row. If these letters are distinct from one another then by the Multiplication Principle, there are 14! different arrangements in all.

But the letters are not all distinct. In fact there are only two kinds – N’s and E’s. This means an arrangement, for example, consisting of 7 N’s followed by 7 E’s,

N E N E N E N E N E N E N E 

has been counted 7!7! times in all in 14!. The same is true for this arrangement:

N N N E E N N E E N N E E E.

Thus, to find the number of ways of arranging 14 letters where 7 of which are identical and the remaining 7 are also identical, 14! need to be divided by 7!7!

If the problem had been In how many ways can you arrange 10 N‘s and 4 E‘s?, the solution will be 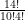\frac {14!}{10!4!}.

Notice that this solution uses the technique of counting the number of permutations (arrangements) of n objects, r1 of which are identical, r2 are identical, . . . , and rn are identical, where r1 + r2 + . . . ri = n. The number of different permutations is denoted by

In the problem, n = 14, r1 = 7 and r2 = 7. Hence, the total number of arrangements is 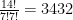 \frac{14!}{7!7!} = 3432.

Solution 2

This solution simplifies the original problem to How many different ways can 7 N’s be arranged in a row of 14 spaces? Now, why is this problem equivalent to the original problem? What happened to the 7 E‘s? Why aren’t they not considered anymore? This is because for a particular arrangement of 7 N‘s in 14 spaces, there is one and only one way the 7E‘s can be arranged.

To solve, count the number of possible positions for the 7 N’s. You have 14 positions to choose from for the first N. For the next N you only have 13 positions to choose from, for the next N, 12 and so on until the 7th N. By the Multiplication Principle you have  14.13.12.11.10.9.8.7 different possible positions where you consider each N to be distinct.

But the N’s are identical. That is, in the arrangement for example

_ N _ N N N _ N N _ _ _ _ N

N has been counted 7! times in 14.13.12.11.10.9.8.7. So you have to divide this by 7!

Thus, there are  different positions for N (all N are identical). This can be written in as shorter way using factorial notation by multiplying it by \frac{7!}{7!}.

If there were 10N‘s and 4 E‘s, the problem would have been In how many ways can I arrange 10 N’s in 14 spaces?

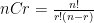In general, if there were n possible positions for arranging r objects, the formula is \frac {n!}{r!(n-r)}. Note that this looks like the combination formula which is used to solve problems for the number of combination and indeed it is. You just got used to applying nCr = \frac {n!}{r!(n-r)} to problems like In how many way can you arrange n different objects taken r objects at a time?